I)         La planification de la production

a)                  L’organisation des projets (PERT et MPM)

La gestion des projets nécessite des outils particuliers d’ordonnancement. On distingue les techniques modernes d’ordonnancement (PERT et MPM) et le diagramme de Gantt qui reste une méthode ancienne mais encore répandue.

Ces techniques d’ordonnancement sont utiliser principalement pour la gestion production type séries unitaire (construction d’un pont, lancement d’un nouveau produit, organisation des jeux olympiques)

b)                 L‘analyse du projet

• Etape N°1 : Etablir la liste des taches ou activité nécessaire a la réalisation du projet.

• Etape N°2 : Evaluer la durée de chacune des taches, ceci n’est pas évident du fait de certaines dépendances extérieures (délai de livraison, condition météo….) et de l’absence d’expérience pour la réalisation de certaines taches.

• Etape N°3 : Repérer les contraintes d’antériorités qui imposent à certaines opérations de ne pouvoir commencer que si d’autres opérations sont terminées (construction d’une maison, les fondations doivent être terminées pour bâtir les murs).

c)                  La méthode PERT (méthode potentiel sommet)

La méthode PERT (Program Evaluation and Review Technic) a été mise au point en 1958 à l’occasion du projet POLARIS (Programme missile à longue porté) par l’US. Ce projet comportait 250 fournisseurs et 900 sous traitants et avait une initiale de 7ans. L’application de la méthode a permis de réduire ce délai à 4 ans.

L’administration fédérale des USA exige que les réponses à certains appels d’offres s’accompagnent d’un ordonnancement utilisant cette technique.

Dans la méthode PEET, les taches sont représentées par des ares dans un réseau. Les sommets du graphe représentant des évènements (étapes) qui matérialisent le début de certaines taches et la fin d’autres taches.

Représentation des taches

Exemple 1 : C succède à A et a B

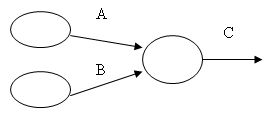
Exemple 2 : D succède à B et à C, et E succède à B

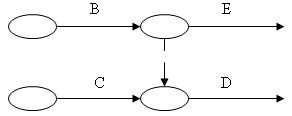
La représentation des contraintes d’antériorité, dans ce cas, nécessite l’introduction d’une tache fictive (en pointillé) dont la durée est nulle.

La résolution d’un problème d’ordonnancement se fait en plusieurs étapes. A partir de l’application qui suit, nous allons suivre l’ensemble des étapes.

Application : Pour la réalisation d’un projet, on vous communique l’ensemble des taches a effectuer, les durées de ses taches et les antériorités a respecter. On vous demande de construire le graphe PERT afin de calculer la durée totale de ce projet et de mettre en évidence les taches critiques.

Etape n°1 :

Etape n°2 :

Tracer du graphe. Le tracé est normalisé

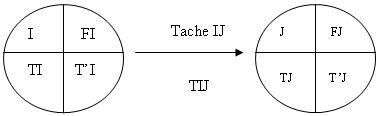
 I : sommet de début de la tache ij

 J : somment de la fin de la tache ij

 TIJ : durée de la tache

 TI, TJ : Date au plutôt

 T’I, T’J : date au plus tard

 FI, FJ : Intervalles de flottement. 

Etape n°3 :

            La date au plutôt d’une étape est la date au plutôt. Certaines tâches sont terminées et où d’autres peuvent commencer. Les dates au plutôt s’obtiennent en recherchant la valeur maximale du chemin allant du Début à Fin. La date au plutôt de l’étape Fin donne la durée minimale de réalisation du projet.

Etape n°4 :

Calcul des dates au plus tard. La date au plus tard d’une étape est la date qu’il ne faut en aucun cas dépasser si l’on veut respecter la durée de réalisation du projet.

Sachant que la date au plus tard de l’étape Fin est égale à la date au plutôt de l’étape Fin. Les autres dates au plus tard s’obtiennent en remontant les arcs et en retranchant les durées. On retiendra à chaque fois les valeurs finies.

Le chemin critique :

Le chemin critique est le chemin le plus long allant Début à Fin. Il passe par les sommets pour lesquels la date au plutôt est égale à la date au plus tard et par les tâches dont les durées ont contribuées au calcul des dates au plutôt.

En additionnant les durées des tâches qui compose ce chemin, on obtient la durée du projet. Ces tâches sont appelées tâches critiques.

Dans l’exemple, il y a 2 chemins critiques : {B,F,K} et {A,D,G,I}. A, D, G, I, B, F et K sont appelées tâches critiques, c’est-à-dire tout retard dans la réalisation de ces tâches se répercutera sur la durée de réalisation du projet.

Etape n°5 : Calcul des intervalles de flottements (Fi)

        L’intervalle de flottement représente le retard permis dans l’attente d’une étape sans que la duré totale du projet soit affectée. L’intervalle de flottement s’obtient en faisant la différence entre la  date  au plus tard et la date au plus tôt

Fi = T’i – Ti

        Ici, l’intervalle de flottement est nul pour toutes les étapes. Ceci est normal dans la mesure où pour atteindre chacune de ces étapes on passe obligatoirement par une tache critique.

Etape n°6 : Calcul des marges libres et totales

        Les marges libres et totales se calculent pour les taches. La marge libre (ML) représente le retard maximum du démarrage d’une tache ij sans que la date de démarrage des autres opérations soit modifiée.

ML (ij) = Tj – Ti –Tij

        La marge totale (MT) représente le retard maximum sur le début d’une tache ij si l’on accepte de repousser les opérations suivantes sans toutes fois allonger la durée totale du projet.

MT (ij) = T’J – Ti - Tij

    La marge totale est la somme de la marge libre de la tache ij et de l'intervalle de flottement de l’étape j.

Remarque : les marges libres et totales critiques sont nulles.

d)        La méthode MPM (Méthode Potentiel Taches)

        La méthode MPM (Méthode Potentiel Métra) a été mise au point par B. Roy (Sema) à l’occasion de la construction du bateau France. Dans cette méthode les taches sont matérialisées par les nœuds (sommets) du réseau. Les arcs représentent quant à eux les relations d’antériorité.

Représentation des taches :

Exemple : D succède à B et à C et E succède à B

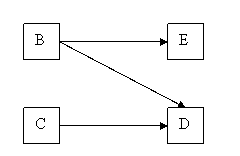
Remarque : il n’y a pas de taches fictives dans la Méthode des Potentiels Métra

Application : Pour la réalisation d’un projet, on vous communique l’ensemble des taches à effectuer, les durées de ces taches et les antériorités à respecter. On vous demande de construire le graphe PERT afin de calculer la durée de ce projet et de mettre en évidence les taches critiques.

Etape n° 1 : Tracé du graphe

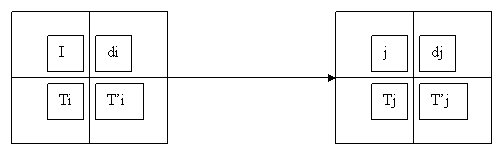
i : Tache

di : durée de la tache i

Ti : date au plus tôt tache i

T’i : date au plus tard tache

Etape n°2 : Calcul de la date au plutôt  (Ti)

        La date au plutôt d’une tache est la date où au plutôt la tache peut débuter. Les dates au plutôt s’obtiennent en recherchant la valeur maximum du chemin allant de Début à Fin. La date au plutôt de Fin donne la durée minimale de réalisation du projet.

Etape n°3 : Calcul de la date au plus tard

        La date au plus tard d’une tache est la date qu’il ne faut en aucun cas dépasser dans le démarrage de la tache s’il on veut respecter la durée de réalisation du projet . Sachant que la date au plus tard de Fin, les autres dates au plus tard s’obtiennent en remontant les arcs et en retranchant les durée. On retiendra chaque fois la valeur minimale.

Chemin critique :

    BFK fin

    ADGI fin    21 jours

Etape n°4 : Calcul de marge

        La marge libre (ML) représente le retard minimum au démarrage d’une tache i sans que la date de démarrage des autres opérations soit modifiée.

ML (tache i) = Min (Tj – Ti – di)

Etape n°5 : Calcul de la marge totale

        La marge totale (MT) représente le retard maximum sur le début d’une tache i. Si l’on accepte de repousser les opérations suivante sans que toute fois allonger la durée totale du projet.

MT (tache i) = T’i – Ti

Etape n°5 : Comparaison des deux méthodes

        Les deux approches fournissent les mêmes résultats, mais la méthode MPM est la plus facile d’utilisation. Le graphe MPM est plus lisible par un non spécialiste. Il facilite la modification du problème par une suppression.